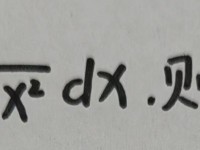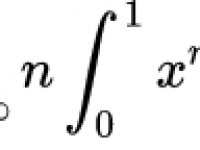提交新的问题
[已解决] 问题303: 设A是mxn矩阵,B是nxm矩阵,E是m阶单位矩阵,若AB=
已解决 · 线性代数 · 昨天 20:54 · 阅读 13[已解决] 问题301: 0.36-(-8.67)÷(-0.3)+0.82
已解决 · 昨天 20:21 · 阅读 113[已解决] 问题299: RSA算法的原理是什么?
RSA原理 已解决 · 初等数论 · 昨天 14:01 · 阅读 17[待解决] 问题297: an=∫x^n√1+x², 则lim n+1an+1/an=?
待解决 ·
昨天 08:34
· 阅读 30
[待解决] 问题296: Consider A,B∈Rn×n . Suppose that A and B are similar. Show that there is an invertible matrix S such that Null(B)={x∈Rn∣∃y∈ Null(A),x=S−1y}
待解决 ·
一天前
· 阅读 27
[已解决] 问题290: (28808)÷124=24000余8
已解决 · 小学数学 · 4天前 · 阅读 61[已解决] 问题288: 两个正方形求一个阴影比另一个阴影面积大多
已解决 · 5天前 · 阅读 60[待解决] 问题286: 求将 y=x3 和 y=4x2 围成的区域绕 y=−1 直线旋转得到的立体体积:
待解决 ·
3天前
· 阅读 69